MM算法思想
MM算法是一种迭代优化方法,它利用函数的凸性来找到它们的最大值或最小值。当目标函数$f(\theta)$较难优化时,算法不直接对目标函数求最优化解,转而寻找一个易于优化的目标函数$g(\theta)$替代,然后对这个替代函数求解,$g(\theta)$的最优解逼近于$f(\theta)$的最优解。每迭代一次,根据所求解构造用于下一次迭代的新的替代函数,然后对新的替代函数最优化求解得到下一次迭代的求解。通过多次迭代,可以得到越来越接近目标函数最优解的解。
MM代表“Majorize-Minimization”或“Minorize-Maximization”,取决于所需的优化是最大化还是最小化。
- Majorize-Minimization:每次迭代找到一个目标函数的上界函数,求上界函数的最小值。
- Minorize-Maximization:每次迭代找到一个目标函数的下界函数,求下界函数的最大值。
期望最大化(EM)算法可以被视为MM算法的特殊情况,在机器学习中经常用到。MM算法与EM算法有联系但是又有区别,在EM算法中通常涉及条件期望,而在MM算法中,凸性和不等式是主要焦点。
以Minorize-Maximization为例, 使目标函数$f(\theta)$最大化。
在算法的第$m(m=0,1…)$步,若满足以下条件,则目标函数$f(\theta_m)$可用构造函数$g_m(\theta_m)$代替。
\[g_m(\theta) \leq f(\theta_m) \ \ \forall \theta\] \[g_m(\theta_m) = f(\theta_m)\]MM算法步骤
- 使$m = 1$,并初始化$\theta_0$。
- 构造$g_m(\theta)$满足条件$(1)$和$(2)$。
- 令$\theta_{m+1}=\arg\underset{\theta }{\mathop{\min }} \ g_m(\theta)$。
- 使$m=m+1$,返回步骤2。
$\theta_m$和目标函数的替代函数的迭代步骤如下图所示。
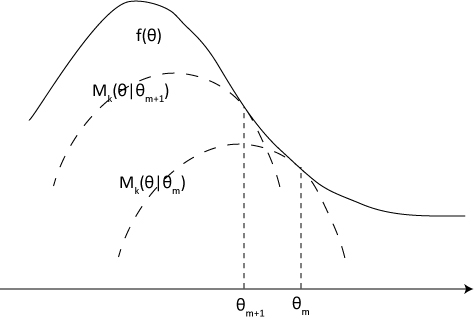
由以上条件可的如下不等式: \(f(\theta_{m+1}) \geq g_m(\theta_{m+1}) \geq g(\theta_m|\theta_m) = f(\theta_m)\)